[Algorithms] 유니온 파인드
[Algorithms] 유니온 파인드
안녕하세요? 정리하는 개발자 워니즈 입니다. 이번 카테고리의 첫 포스팅은 알고리즘의 주제인 유니온 파인드에 대해서 해볼까 합니다. 유니온 파인드는 Disjoint Set이라고도 불리우며, 이 자료구조는 우리 일상속에서 손쉽게 볼 수 있습니다.
예를들어, 어려서 놀이시간에 노래를 틀어두고 몇명 모여라! 라는 게임을 해본적이 있을것입니다. 이런게임이 바로 유니온 파인드의 개념이 들어가있는 것입니다.
처음에는 각각 1명씩 개별적인 트리입니다. 그리고 1명이기 때문에 상위에는 누군가가 존재하지도 않는 독립적인 존재입니다. 그러다가 명수에 맞춰 합치게 되면, 트리구조에 맞춰 상위의 노드가 존재하게 됩니다.
1. 초기화 과정
for (int i = 1; i <= n; i++) {
parent[i] = i;
level[i] = 1;
}
UNION-FIND 함수에서는 parent 배열이 중요합니다. 초기는 자기 자신이 루트 노드가 됩니다.
2. FIND 함수
public static int find(int u){
if(u == parent[u])
return u;
return parent[u] = find(parent[u]);
}
find함수는 위와 같이 간단하게 처리가 될 수 있습니다.
u와 parent[u]가 같은지 부분은 결국 루트노드가 자기 자신이냐를 묻는 조건입니다. 그렇다면, 자기 자신을 return 하게 되고, 아니라면, parent[u] = find(parent[u])을 호출하게 됩니다.
find함수에서 parent(상위노드)를 계속해서 거슬러 올라가게 되고, 최상위 까지 올라가서 결국에 자기자신이 parent이면, return을 해주는 구조입니다.
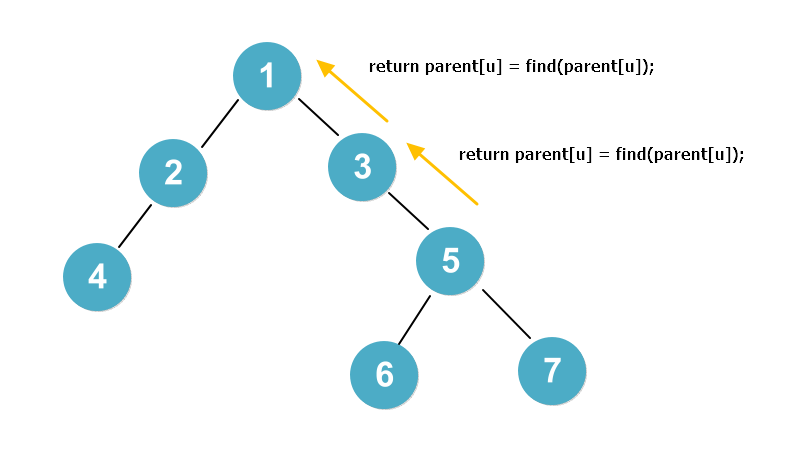
5번 노드에 대한 find 탐색을 시도하면, 위로 2번 거슬러 올라가서 1번 노트가 parent라는 것을 알려줍니다.
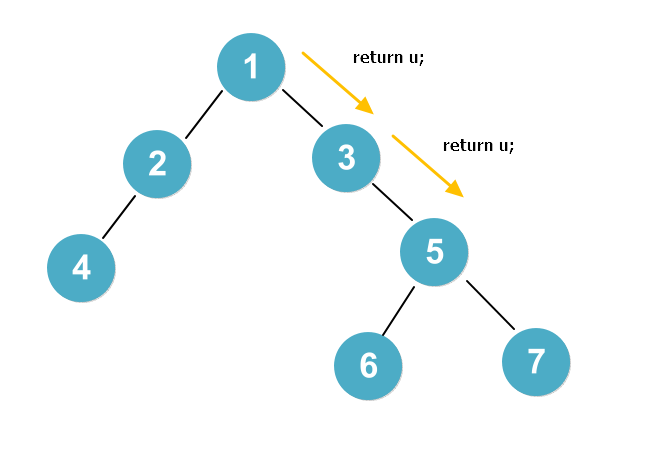
return을 주는 가운데, 3번 노드에게도 1번이 parent이고, 5번 노드에게도 1번이 parent라고 셋팅을 하게 됩니다. 그렇게 되면 다음과 같이 경로 압축 과정을 거치게 됩니다 .
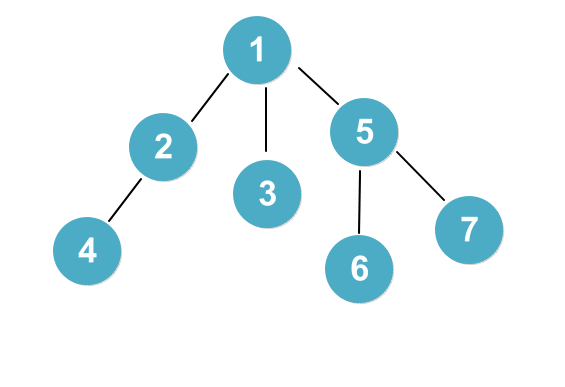
3. UNION 함수
public static void merge(int u, int v){
u = find(u);
v = find(v);
if(u==v) return;
if(level[u] > level[v]) swap(u, v);
parent[u] = v;
if(level[u] == level[v]) ++level[v];
}
유니온 함수는 크게는 다음의 로직으로 진행됩니다.
- u,v의 루트 노드를 찾아 나갑니다.
- 두개의 루트노드가 일치 한다면, merge가 된 상태이기 떄문에 return 합니다.
여기서 아닌 경우가 중요합니다.
parent[u] = v; 이부분의 의미는 u의 부모를 v로 삼겠다는 것입니다. 즉 v가 u의 루트 노드가 되는 것입니다. 그런데 중간에 level을 체크해주는 로직이 들어갑니다.
- if(level[u] > level[v]) swap(u, v);
merge가 되는 과정에서 효율적으로 merge를 하기 위해서는 깊이(level)가 큰 것에 작은것이 들어가는 것이 좋습니다. u가 무조건 v의 자식이 되고, v는 u의 부모가 되는 구조로 잡았기 때문에 level을 체크해서 swap을 해줍니다.
- level[u]와 level[v]가 같다면, ++level[v];
만약 두개의 level이 같다면 v를 더 크게 유지해줍니다.
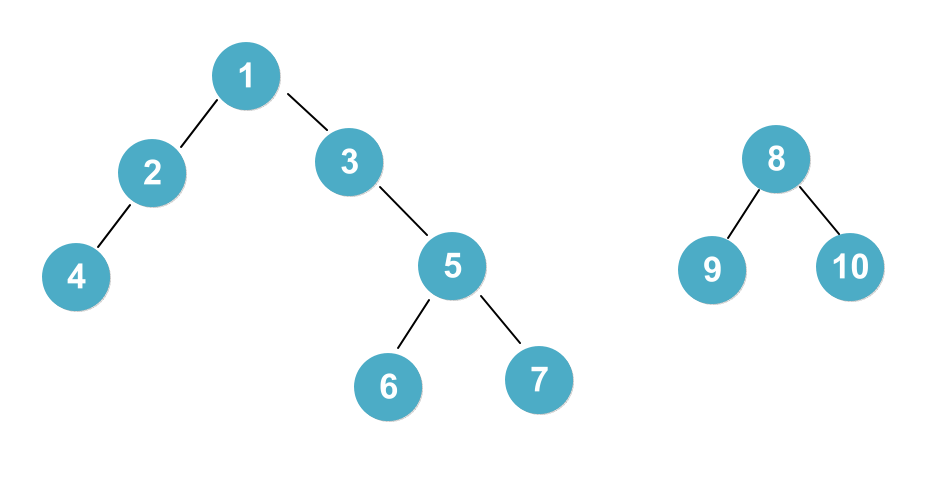
예를들어, 위와 같이 2개의 트리가 있다고 가정해봅시다.
5번과 9번 노드를 합치는 과정을 거친다면, 각각의 find과정을 거쳐서 최상단의 parent 노드를 찾게 됩니다.
그런데 2개의 노드를 합치는 과정에서 중요한것이, u가 무조건 더 작은 트리가 되도록 셋팅을 하는 것입니다.
그래서 level을 체크하고, u가 더 깊은 노드라면, u,v를 swap한뒤, 큰트리의 루트노트가 작은 트리의 루트노드의 부모가 됩니다.
위의 예시에서는 u,v의 루트 노드인 1과 8이 각각 u와 v로 셋팅이 되었는데, 실제로, u가 v보다 깊은 트리이기 떄문에 루트노드를 swap합니다.
그리고 (1,9,10)으로 구성된 트리가 8의 아래로 들어가면서 최종적으로는 아래와 같은 그림이 됩니다.
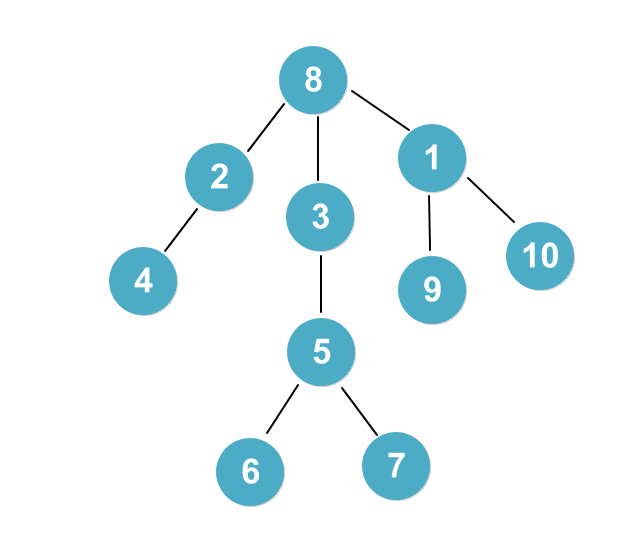
4. 관련 알고리즘 문제
관련한 알고리즘 문제는 위와 같이 있고, 필자는 java를 이용해서 여행가자문제를 풀었습니다. 관련한 내용은 아래에 있습니다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class UNION_1976 {
static int n,m; //도시의수, 여행계획 도시의 수
static int[] parent,level,route;
static int[][] city;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(br.readLine());
m = Integer.parseInt(br.readLine());
parent = new int[n+1];
level = new int[n+1];
route = new int[m];
city = new int[n+1][n+1];
for (int i = 1; i <= n; i++) {
parent[i] = i;
level[i] = 1;
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= n; j++) {
city[i][j] = Integer.parseInt(st.nextToken());
}
}
st = new StringTokenizer(br.readLine());
for (int i = 0; i < m; i++) {
route[i] = Integer.parseInt(st.nextToken());
}
/* 도시 연결 */
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (city[i][j] == 1) {
merge(i, j);
}
}
}
boolean chk = true;
int u = find(route[0]);
for (int i = 0; i < route.length; i++) {
if (u != find(route[i])) {
chk = false;
}
}
System.out.println(chk ? "YES" : "NO");
}
public static int find(int u){
if(u == parent[u])
return u;
return parent[u] = find(parent[u]);
}
public static void merge(int u, int v){
u = find(u);
v = find(v);
if(u==v) return;
//if(level[u] > level[v]) swap(u, v);
parent[u] = v;
//if(level[u] == level[v]) ++level[v];
}
public static void swap(int a, int b){
int t = a;
a = b;
b = t;
}
}
5. 마치며...
유니온 파인드를 통해서 적절하게 필요한 노드들을 묶어주고 연결이 되어있는지를 체크하는 문제에서 활용될 알고리즘들입니다. union함수와 find함수는 필수적으로 기억해야 될 것입니다.
